Beneath the LLMs

2/13/2025

It is unwise for mortal man to attempt the understanding of that, which is beyond his conception, for there lies the road to disbelief and madness. Yet, man is man and ever fated to reach out beyond himself, striving to attain things which always just elude his grasp. So in his frustration, he replaces the dimly seen incomprehensible with things within his understanding. If these things but poorly reflect reality, then is not the reflection of reality, distorted though it may be, of greater value than no reflection at all?
CRT 1:1

本文试图展示一部分 transformer 的图景，帮助我可爱的朋友们在无需了解公式的情况下快速建立起 LLM 如何工作的直觉，同时给已经了解 transformer 的朋友们带来新的观点。

Transformer

Embedding

如果我们希望计算机能处理某个现实事物，我们就得把它「编码」到计算机能处理的「语言」上。Embedding 层的作用就是把输入的文本序列映射到计算机能处理的数字上。

当然，最简单的方式就是我们给每个词元（以下称为 token）都分配一个编号：猫是 1，鱼是 2，吃是 3...

假如输入了一个句子「猫吃鱼」，我们就在字典中进匹配¹，得到句子的编码 $[1, 3, 2]$ ，这样我们就完成了分词（tokenization）过程，可以将其送往下一层的自注意力 (Attention) 层了。

That's all! 看起来我们似乎不需要用上什么 Embedding 模型？

理论上来说的确是这样的。只要 Attention 层表达能力足够强，它应该可以从这些毫无关联的编号中学习到不同 token 间的共现模式、上下文关系，隐式地构建出对语义信息的理解。但我们会遇到许多问题：

为了充分利用 GPU，我们的 Attention 不能进行过于复杂的计算，这一定程度上限制了 Attention 层的表达力
模型无法对词表外的新词泛化，需要重新训练才能理解新词和其他词汇的语义关系
模型在学习上下文关系同时还要学习词汇本身之间的关系，这会让模型训练变得更加困难

不妨我们做一些预处理，把「理解 token 之间的语义关系」的功能从后面的流程中分离出来²，预先计算出每个 token 的某种语义表示。在我们假想的词语空间中，相关的词应该彼此「距离」非常近，无关的词应该「距离」更远。现在我们要来找到一种合适的，计算机能处理的「表示」来满足这个条件。首先让我们来想象一下，如果把每个 token 都映射到一个实数上，并保持「相关的词距离相近」的原则，会发生什么呢？

假如我们有一个词语「狼=0.1」，为了保持「狼」和「狗」的距离，我们得给「狗」分配一个接近 0.1 的值，比如「狗=0.11」。同时狼应当与「攻击性」接近，为了保持「狼」和「攻击性」的距离，我们让「攻击性=0.09」。狼与月亮也应当相近，但无论月亮放在哪里，月亮都会与其他的词关联上：要么月亮具有攻击性，要么狗会在月光下长嚎。

我们得用很多个数来表示一个词，才能保持「相关的词距离相近，不相关的词距离远」的结构。很多个数组合在一起就是一个向量。那么我们需要多少个数来编码一个词呢？

虽然我们的词表可能有数十万个词元，向量的维度 $n$ 并不需要那么大，因为 $n$ 个维度可以编码 $2^{n-1}$ 个相互正交的方向（指数的力量！想想用 10 只老鼠就可以找出 1000 瓶水中的一瓶毒药），而模型可以容忍一定程度的误差——实际上还可以装得下更多。

通过向量来编码词，然后用向量的点积作为两个词语相似性的度量，我们就可以通过机器学习来得到一个合适的 Embedding 模型。

这里为什么是点积（某种程度上衡量的是向量之间的夹角大小）而不是向量之间的距离呢？这其实是一种维度诅咒：高维空间中，均匀随机分布的所有数据点之间的距离都趋于同样的值。虽然数学上距离仍然有效，但我们的计算精度毕竟是有限的，使用角度作为相似性的度量则没有这个问题。给定两个向量 $\textbf{x}=[x_1, x_2, ..., x_n]$ 和 $\textbf{y}=[y_1, y_2, ..., y_n]$ ，我们有这样的公式：

similarity = cos(\theta) = \frac{\textbf{x}\cdot\textbf{y}}{\lVert \textbf{x} \rVert \lVert \textbf{y} \rVert}

维度诅咒让 $\lVert \textbf{x} \rVert$ 和 $\lVert \textbf{y} \rVert$ 也趋于常数，所以我们只需要计算向量的点积，就可以得到两个向量之间的相似性。

Embedding 层的作用就是查表，在 Embedding 模型（一个大矩阵，或者说 map<token_id, vector>）中找到每个词元对应的 $n$ 维向量。Embedding 这个名字来源于数学中的「嵌入」：从对象 $X$ 到对象 $Y$ 的保持结构的单射——在这里是 $\big(\text{词元(集合)}, \text{语义相似程度(结构)}\big) \to \big(\text{向量(集合)}, \text{向量的内积(结构)}\big)$ 。³

Attention

接下来就是 Transformer 的核心部分之一了：多头自注意力层。我们先来理解「注意力」是什么。

~~它说白了不过就是在 Comonad 上进行 extend：~~

class Functor w => Comonad w where
    extract   :: w a -> a
    duplicate :: w a -> w (w a)
    extend    :: (w a -> b) -> w a -> w b
selfAttention :: Comonad w => w a -> w a
selfAttention = extend f
  where
    f :: w a -> a
    f ctx =
        let q = extract ctx
            ctxs = duplicate ctx
            scores = score q (fmap extract ctxs)
            weights = softmax scores
        in combine weights (fmap extract ctxs)

class Functor w => Comonad w where
    extract   :: w a -> a
    duplicate :: w a -> w (w a)
    extend    :: (w a -> b) -> w a -> w b
selfAttention :: Comonad w => w a -> w a
selfAttention = extend f
  where
    f :: w a -> a
    f ctx =
        let q = extract ctx
            ctxs = duplicate ctx
            scores = score q (fmap extract ctxs)
            weights = softmax scores
        in combine weights (fmap extract ctxs)

好了，我们不玩抽象废话梗了，希望理解的朋友可以询问 AI。想象这样一个场景：你打开微信突然看到一张微笑表情。你虎躯一震，目光开始游走，最终锁定在了发送人的昵称上：张老师。

Attention 正是这样工作的：对于输入序列里的每个词（比如，微笑脸），扫一遍整个上下文，确定应该关注哪些词（发送人），然后根据需要关注的词细化自己的语义（长辈发送的微笑脸）。

假如我们直接用 Embedding 模型输出的向量和语义相似度来确定应该关注哪些词呢？那么按照 Embedding 的设计，和「微笑脸」语义相似的应该是其他表情：「大笑」「哭笑不得」，在观察上下文的时候只会注意到和自己语义相近的词，而不会注意到「张老师」。这要不得！

好，现在我们把「词语应该在上下文关注哪些词」和「词语的实际语义」解耦，对于每一个输入的向量 $\textbf{x}$ ，我们用两个函数

\begin{aligned} Query &= q(\textbf{x}) \\ Value &= v(\textbf{x}) \\ \end{aligned}

来分别得到 Query、Value 两个向量。对于每个词 $\textbf{x}$ ，我们在上下文中寻找和 $q(\textbf{x})$ 最相似的 $q(\textbf{y})$ ，然后根据相似度 $similarity(q(\textbf{x}), q(\textbf{y}))$ 来更新 $v(\textbf{x})$ 的语义：

v'(\textbf{x}) = v(\textbf{x}) + similarity(q(\textbf{x}), q(\textbf{y})) \cdot v(\textbf{y})

我们把这个假想的架构叫做 QQV，年轻人的第一款 naive 注意力。很快我们就会发现不对劲：

当我们看到「微笑脸」的时候，我们希望找到发送人是谁
而我们看到「张老师」的时候，我们不会尝试在上下文中寻找「微笑脸」，因为它不会为「张老师」提供任何额外的信息

这种词语之间的相互关注关系是不对称的。每一个词在上下文中扮演了几个不同的角色：

Q(Query): 我需要关注哪些方面的信息？
K(Key): 我提供哪些方面的信息？
V(Value): 我提供的信息内容是什么？

实际上我们要用三个函数，把 Embedding 层输出的向量分别映射到 Query/Key、Value 两个空间上。⁴

\begin{aligned} \text{Query}(\textbf{x}) &= \textbf{x}\cdot\textbf{W}_Q \\ \text{Key}(\textbf{x}) &= \textbf{x}\cdot\textbf{W}_K \\ \text{Value}(\textbf{x}) &= \textbf{x}\cdot\textbf{W}_V \end{aligned}

这里 $W_Q$ 、 $W_K$ 、 $W_V$ 是三个可以被学习的矩阵（线性变换），它们就是用来把 $\textbf{x}$ 映射到 Query/Key/Value 空间上的函数（为什么是矩阵乘法呢？还是因为它容易学习也方便计算）。Query, Key, Value 是三个向量。

对于某个输入向量 $\textbf{x}$ ，我们在上下文中寻找和 $q(\textbf{x})$ 最相似的 $q(\textbf{y})$ ，然后把相似度作为权重来更新 $v(\textbf{x})$ 的语义。

\text{new\_semantic}(\textbf{x}) = \sum_{i=1}^{n} \text{similarity}(\textbf{x}, \textbf{y}_i) \cdot \text{Value}(\textbf{y}_i)

这个新的语义向量被编码了额外的上下文的信息，它解释起来可能像这样：

「他邪魅一笑三分神秘,三分诱惑,还有四分不可捉摸的邪气」。

实际上的 Attention 公式计算所有位置的注意力分数（矩阵乘法=同时计算所有行向量和列向量的点积），把相似度归一化到 $[0, 1]$ 之间作为权重，然后按权重加权求和。

\begin{aligned} \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right) \cdot V \\ \begin{aligned} Q &= \left[Query(\textbf{x}_1), Query(\textbf{x}_2), ..., Query(\textbf{x}_n)\right] \\ K &= \left[Key(\textbf{x}_1), Key(\textbf{x}_2), ..., Key(\textbf{x}_n)\right] \\ V &= \left[Value(\textbf{x}_1), Value(\textbf{x}_2), ..., Value(\textbf{x}_n)\right] \end{aligned} \end{aligned}

其中 $Q$ , $K$ , $V$ 是每个位置的 Query、Key、Value 向量拼接到一起变成的矩阵。softmax 是个把一组输入映射到 $[0, 1]$ 之间并满足 $\sum_{i=1}^{n} \text{softmax}(x_i) = 1$ 的函数。 $\sqrt{d_k}$ 是随维度变大的缩放因子，用来防止点积过大⁵导致 softmax 输出的概率过于集中。

一个句子中词语之间的关系不止一种，有语法结构上的，有语义上的，有因果逻辑的。多头注意力就是用多个不同的脑袋以不同角度关注上下文的不同方面（并行计算多个不同的 QKV，然后拼接起来），增强模型捕捉词语之间不同关系的能力。

在进入下一层之前，让我们先来总结一下 Attention 层：

输入：Embedding 层输出的语义向量序列
输出：被上下文丰富后的语义向量序列
训练：模型学习到每个词语需要关注哪些信息、提供哪些信息、具体语义的表示，即 $W_Q$ 、 $W_K$ 、 $W_V$ 三个线性变换
中间过程：
- 每个位置输入语义向量映射到 Query、Key、Value 向量
- 计算注意力
- 按注意力分数加权求和
- 把多个注意力头拼接起来
- 通过一个线性变换得到最终的输出

虽然输入和输出都是向量序列，但我们可以发现注意力计算的时候并没有考虑序列的顺序，这样会导致模型无法区分「猫吃鱼」和「鱼吃猫」。所以在 Embedding 层之后，我们还需要一个位置编码层，来给每个位置的向量加上位置信息。比如常用的 RoPE 位置编码，就是把原始向量的每两个分量按下标 $i$ 旋转一个角度 $\theta_i = \frac{k^{2i/d}}{k}$ ( $k$ 是常数，一般 $k=10000$ ， $d$ 是向量维度)，这样模型就能够区分不同位置的向量了。

当然，在 Decoder-only 的 LLM 中，我们还有一个特殊的掩码机制「因果掩码」（Causal Mask）。在计算注意力时，会屏蔽掉当前位置之后的 token。也就是模型只能根据上文对当前 token 补充信息，在预测下一个 token 时，也只能依赖于已经生成的 token (上文)。同时由于因果掩码的存在，每个位置 token 的注意力计算之后就不会发生变化了，可以被缓存下一次计算的时候直接使用（KV Cache）加快计算速度。

Feed-Forward Network

猜猜 LLM 中，参数量最多的层是什么？答案是 FFN。

FFN 常常在讲解 Transformer 的文章中被忽略，实际上 Attention 层和 FFN 层是 Transformer 中最重要的两个部分，共同决定了 Transformer 的性能。缺了 FFN，Transformer 就很难正常工作了。但它的结构其实很简单：

\text{FFN}(x) = \text{Activation}(\textbf{x}\textbf{W}_1 + \textbf{b}_1)\textbf{W}_2 + \textbf{b}_2

对于 Attention 输出的语义向量序列中的每个向量，FFN 层会

把向量映射到高维空间
通过 Activation 激活函数
把向量映射回低维空间

这样讲太抽象了，我们稍微具象一点。在原始 Transformer 论文中，激活函数是 ReLU，我们也以它为例。

ReLU 是什么？什么是激活？

\text{ReLU}(x) = \begin{cases} x, & \text{if } x > 0 \\ 0, & \text{if } x \leq 0 \end{cases}

所谓的「激活」，就是输入的信号满足特定条件时，激活函数产生输出信号；否则抑制输出。

对一个一维的 ReLU 函数，输入的信号满足 $x > 0$ 时，输出 $x$ ，否则抑制输入信号。

ReLU

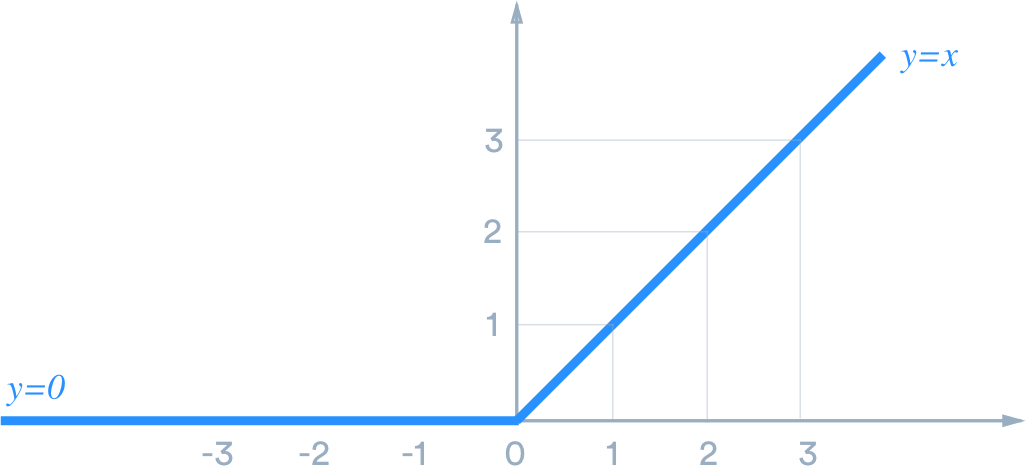
在二维空间中，ReLU 激活函数定义了一条直线边界，将空间划分为两部分：边界一侧信号被抑制 (输出 0) ，另一侧信号被保留 (输出原始值)

ReLU 在 FFN 中做了什么？

每一个 ReLU 连同升维使用的线性变换和偏置一起，维护了一个 $n-1$ 维的超平面，把输入空间分成了两部分。

这个超平面等价于一个条件判断：一个极度复杂抽象的 if 语句。Attention 输出了一个语义向量的序列，对这个序列中的每一个向量，FFN 层中的 $d_{ff}$ 个 ReLU 函数都判断输入向量是否满足自己的边界条件，决定是否「激活」。以最近火热的 DeepSeek-R1 为例，它的 FFN 有 $18432$ 个 SiLU 函数，有 $61$ 个 Attention-FFN 块，相当于每个向量都会经过 $61*18432= 1,124,352$ 次激活函数的判断，而每次判断又包含向量维度（在 R1 中是 $7168$ ）那么多个条件——我们一共有 80 亿个 if。写过屎山的朋友们都知道，只要 if 足够多，再复杂的业务系统都可以表达出来。（现在知道为什么 LLM 开销那么大了吧）

每个 ReLU 的边界所代表的条件，不只是「这个词是否与动物有关」这样简单的判断，一个 ReLU 的边界可以同时判断多个（几乎正交的）特征。而判断的内容也不一定是某种具体的概念或者知识，实际上我们对它所表征的东西几乎一无所知。

为什么要升维？

维度变高之后，向量分布会更加稀疏（维度的诅咒，在另一些时候又是一种祝福）。在低维空间中原本线性不可分的数据点，到了高维空间中或许就变得线性可分了。

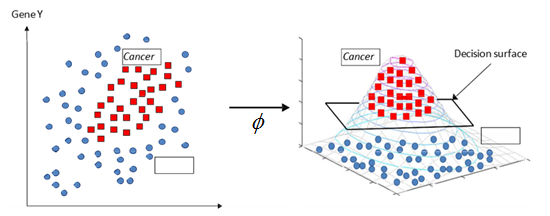
SVM 升维

（图取自支持向量机 SVM 的 Kernel Trick，虽然两者的升维机制有所区别。此图使用的核函数 $\phi=(x,y,x^2+y^2)$ 是非线性的，而 FFN 的升维是线性的）

在左图的二维平面上，我们没有办法一刀切（线性可分）区分出癌症和非癌症的样本，然而在右图的三维空间中，我们可以通过一个平面把两类数据点分开。

再想象另外一个场景：虽然我们没有办法通过一个平面区分出桌子和抽屉，但是如果我们加入一个时间维度 $t$ ，把桌子放到 $t=-1$ 时刻，抽屉放到 $t=1$ 时刻，它们不就可以被一个简单的平面 $t=0$ 分开了吗？

你知道吗？四维的绳子从不打结、我的房间也不曾乱过。低维的眼睛，分辨不出高维的风景。

正好，ReLU 通过一个超平面把输入空间劈成了两部分，我们就提取出了输入向量「是否满足某个特征」。

为什么要降维？

因为残差连接要求输入和输出维度相同。当然降维也带来额外的好处：ReLU 会丢弃掉一部分不相关的信息，使升维后的向量编码的信息量变少，那么更高的维度就有些冗余了。降回最初的尺寸，可以减少维度冗余带来的计算开销。

记忆

若向量编码语义，那么流形刻画知识。

如果我们能够用向量表示语义，「巴黎是法国首都」可以对应一个向量，「巴黎是德国首都」也可以对应一个向量。但我们都知道，只有其中一个向量描述了「事实」。所有作为事实的向量的集合，构成了知识的形状，也是模型学习的目标。

我们可以想象这个形状是怪异的，其上布满了随机性的棘刺。并非所有知识都是非黑即白的「事实」，「知识的形状」也不是静态的，训练数据中可能有噪声或谬误——甚至连事实本身，也并非必然作为事实存在。

FFN 以粗糙的、由简单函数构筑的图册记录与世界相关的知识：某届奥运会中国赢了多少金牌、李白所写下的诗歌、《盗梦空间》讲了一个什么样的故事...在看到「张老师发送的微笑脸」之后，你也需要回忆起来张老师是已经年近花甲还是不满而立，才能理解这个表情的准确含义。

所以说 FFN 也是一种记忆网络，这是完全正确的。⁶

泛化

即使输入向量不在训练集中，升维变换也能照常进行，ReLU 仍能进行判断。这带来了泛化能力，使模型能够外推其学到的知识并能够回答数据集中不存在的问题。

然而泛化也与幻觉相伴相随，过度的泛化（比如输入离训练集的样本非常远）使模型可能会给出一些看似合理但实际不正确的答案。参数量更大的模型和更多样的训练数据可以编码更多的知识，构建起更准确的边界（这也就是参数和训练数据的 scaling law），但仍然无法让模型回答「我不知道」——FFN 对输入的响应是全局的，模型没有办法拒绝任何输入。

混合

前面我们的 Attention 把输入的语义向量叠加了上下文的信息，但同一个语义向量内部的语义之间的关系并没有被考虑，它还不具备复杂的复合语义。

「让我康康」字面上完全读不通，但 FFN 见到这个上下文中的「康」会想起「杰哥不要」「康康你的」，从而理解到「康」是「看」的谐音，把向量映射到更贴合合上下文的语义上（或许还会附带上回想起的梗的信息）。

降噪

一个不太被人注意到的作用：从信息的角度看，ReLU 某种意义上可以看作一个降噪器。输入的信息经过注意力后会混合上下文信息，如果没有 FFN，那么经过多层 Attention 之后，输出的语义向量会混合过多上下文信息变得非常相似，模型会难以区分不同的 token 所表示的语义（Token Uniformity）。

线性变换本身是无法有效消除信息的，「无法有效消除」并非是线性变换不会有信息损失，而是这样的信息损失往往以某些维度的信息全部丢失为代价。而 ReLU 的非线性可以有选择性地保留重要信息，从而在一定程度上消除噪声，让每个 token 保持其独特的特征，与其他的 token 区分开来。

这个过程就是一种特征分离：通过抑制不重要的信息，达到分离、突出关键信息的目的，从而改善整体表征的多样性和区分度。

Add & Norm

这部分对理解 LLM 如何推理不太重要，可以跳过

Attention and FFN is not all what you need. 虽然理论上 Attention 和 FFN 就足够了，但实际上如果没有残差连接（Residual Connection，或者说 Add），模型训练很容易失败。

我们来简单看看为什么残差连接会有用。模型层数越多，它就越能表达更复杂抽象的概念，但深层的神经网络会有一个问题：梯度消失。我们的模型在训练的时候是通过一个叫反向传播的算法计算梯度更新模型参数的，求梯度的链式法则公式长这样（假设每一层对应一个函数 $\textbf{F}_i(\textbf{x}, \textbf{w}_i)$ ）：

\frac{\partial \mathcal{L}}{\partial \textbf{w}_i} = \frac{\partial \mathcal{L}}{\partial \textbf{F}_{n}} \cdot \frac{\partial \textbf{F}_{n}}{\partial \textbf{F}_{n-1}} \cdot \frac{\partial \textbf{F}_{n-1}}{\partial \textbf{F}_{n-2}} \cdot \frac{\partial \textbf{F}_{n-2}}{\partial \textbf{F}_{n-3}} \cdots \frac{\partial \textbf{F}_{i+1}}{\partial \textbf{F}_i} \cdot \frac{\partial \textbf{F}_i}{\partial \textbf{w}_i}

反向传播把要更新层的权重当作变量求偏导，如果 $\frac{\partial \mathcal{F_i}}{\partial \mathcal{F_{i-1}}}$ 小于 1，那么梯度就会越来越小，最后趋近于 0，导致我们很难更新到浅层网络的参数。

Residual 的计算非常简单，就是把输入加上输出作为新的输出

\mathcal{F}_i(\textbf{x}) = \textbf{F}_i(\textbf{x}) + \textbf{x}

或者说（记得 $\textbf{x}$ 是上一层 $\mathcal{F}_{i-1}$ 的输出）

\mathcal{F}_i(\textbf{x}) = \textbf{F}_i(\mathcal{F}_{i-1}(...)) + \mathcal{F}_{i-1}(...)

加上之后，每一层反向传播的时候梯度就变成了下面这样，至少会有 $1$ 的梯度，连乘之后梯度也不会趋近于 $0$ 。

\frac{\partial \mathcal{F}_i}{\partial \textbf{x}} = \frac{\partial \mathcal{F}_{i-1}}{\partial \textbf{x}} + \frac{\partial \textbf{F}_i}{\partial \textbf{x}} = \frac{\partial \textbf{F}_i}{\partial \textbf{x}} + \textbf{I}

想象一根一端固定的非常长的松弛的绳子，现在用手轻轻拉绳子的另一端，我们会发现绳子另一端几乎不怎么运动。而把绳子换成一个硬直杆，那么杆上的每一点都会获得相同的角位移。残差连接就像把柔软的绳子拉紧（或者更严格地说，把绳子分成 N 段并在每段上绑铁条并且通过铰链连接起来），给模型提供了一定的「刚性」，让反向传播能顺利把梯度传回另一端。

而 Norm 也是一种正则化手段，它把输入向量归一化到单位球上，让所有特征都在相同的中心和尺度下参与计算。这更容易理解：如果要用积木搭几十层的高楼，那么你最好保证每一层积木重心都对齐。

残差连接与归一化层如同构建摩天大楼的脚手架，支撑着数十层乃至数百层的深度神经网络，使模型在茫茫参数空间中不致迷失方向。但训练完成过后脚手架仍不能拆掉，它们融入了模型结构，成为了模型本身的一部分。

Output

Transformer

在经历一串 Decoder 层之后，我们得到了一个最终的语义向量序列，这个序列的最后一个向量包含了生成下一个 token 需要的信息。

我们把最后一个向量输入到一个转换语义向量回 token 的线性层（LM Head）。不过和 embedding 不一样的是，这个向量编码的信息太多了（下一个 token 有这些那些含义），映射回来的时候只能得一个 logits 向量，每个分量对应一个词「xxx 有多适配这个语境」。我们用 softmax 函数把这个适配度变成一个概率分布，从中选择一个作为预测的下一个 token，这个过程叫「采样」。

假如每次都把概率最大的作为下一个 token，这样可以吗？当然是可以的，但效果非常一般：如果问同样的问题，永远只能得到同样的答案。我们最好还是按照预测的概率分布从中随机选择 token，这样每次的输出都会不一样。

我们有几种主要的采样方式：

温度采样：通过调整一个叫做「温度 (temperature)」的参数来平滑或锐化概率分布。
- 温度较低会使概率分布更集中，更倾向于选择高概率 token
- 温度较高会使概率分布更平滑，增加选择低概率 token 的机会
Top-k 采样：只从概率最高的 $k$ 个 token 中进行采样。这可以减少低概率 token 的影响，同时保持一定的随机性。
核采样 (Nucleus Sampling / Top-p Sampling): 选择一个最小的 token 集合：其累积概率超过一个阈值 $p$ (例如， $p=0.9$ )，然后从这个集合中采样。这种方法可以动态地调整采样范围，更加灵活。

值得一提的是 temperature，毕竟作为 prompt 工程师，我们得经常和它打交道。在大部分地方，高 temperature 都被描述成「更有创造力、更多样”，低 temperature 被描述成「更保守、更可预测”。但这只是它的一个表面现象，没有其他词能比温度本身更准确地描述这个超参数的作用。

我试图找到一个形象的现象来描述温度的作用，一开始我想到的是「波函数穿过有限/无限深势垒」，但和一众模型讨论了以后认为这个现象不太合适（毕竟量子力学中许多现象无法对应回 LLM）。再然后我们讨论到「随机热力学」，讨论到「玻尔兹曼分布」...等一下，这不就是 2024 年诺贝尔物理学奖的主题「玻尔兹曼机」吗？

的确，用于采样的带温度的 softmax 函数正来自于随机热力学中的玻尔兹曼分布。在 LLM 中，我们可以将模型预测的 token 概率分布看作某种概率景观（势能景观）。高概率的 token 对应于概率景观的「山谷」，而低概率的 token 对应于「山峰」。(更准确地说，应该是「负对数概率」对应「势能」，但为了方便类比，我们用概率大小反向类比势能高低) 。

如果要生成一个以低概率词开头的句子，意味着模型需要逆着概率梯度，就像粒子要爬上势能面的山坡，这需要额外的能量或激励。这种激励可以来自于：

上下文的引导: 特定的上下文可能会强制模型生成一些在一般情况下概率较低的词。
随机性: 基于玻尔兹曼分布进行采样的随机性，允许模型在一定程度上忽略概率最高的路径，选择概率稍低的词。

更高的温度削峰填谷，使山峰变为丘陵，沟壑化为平地。这让模型有更大概率跳出局部的极值，但它的作用也是双面的：一方面，模型有更大概率跳出局部的极值，另一方面，跳入的新极值也不一定是全局最优解。模型有时会陷入复读机状态，就是跳入了一个局部深渊，生成其他 token 的概率过小以至于困在里面出不来了。

说「模型只是按照概率大小猜测下一个 token，它不理解自己在说什么」其实过度简化了 LLM，把它当成了一个纯粹基于频率的马尔可夫过程——如果真是如此，那 n-gram 模型早已独步天下，何须 Transformer 大放异彩？

它是靠记住答案吗？一定程度上是的。但面对没有见过的问题，它也能联系已经学到的知识给出解答，这已经超出了记住的范畴。只有理解了学习过的内容，才能够为符合语境且正确的 token 赋予更高的概率，在各种测试中拿到高分，畅想出合乎逻辑的「慈禧太后逼乾隆皇帝吃饺子」的画面。我们并不能宣称理解不完全就是完全不理解，否则，课本上已给出所有知识点，为何有人无法在考试中取得及格？是还未涌现出智能吗？

我让 DeepSeek R1 翻译了文章开头的引文。

It is unwise for mortal man to attempt the understanding of that, which is beyond his conception, for there lies the road to disbelief and madness. Yet, man is man and ever fated to reach out beyond himself, striving to attain things which always just elude his grasp. So in his frustration, he replaces the dimly seen incomprehensible with things within his understanding. If these things but poorly reflect reality, then is not the reflection of reality, distorted though it may be, of greater value than no reflection at all?
凡人以智识丈量彼岸玄境实乃愚妄，此途险隘直通天地道心崩摧之境。然人性予秉神火，魂灵永被命运丝弦牵引，总向着雾霭尽处似有若无的光辉踉跄攀援。偏是这满腔倔强，将目力难及的迷蒙虚妄尽数打碎，把亘古长夜里的宇宙谜题，悉数敲凿成凡尘巷陌的圆月残砖 —— 云巅之上的万壑幽深，须借红尘市井的檐角蟾光言说；星辰湮灭时的永劫回响，化为灶膛里荻花爆裂时昙花一现的光影流连。此举既是夸父追日的壮烈史诗，亦是飞蛾扑火的凄美寓言，执念与顿悟交织的永恒迷局中，众生皆用触手可及的真实沙砾，替代那些模糊难辨的虚无星屑。此为人类荣耀的铭章，亦是我们永恒的桎梏。

翻译得略显油腻，但我注意到了一个未在原文出现的意象。我没有搜索到这个词组的任何来源，问祂来自什么典故，祂回答：

此四字虽非直接援引某一典籍原文，却是对中国古典宇宙观的创造性抒写。在《周易・系辞》有云：“阴阳不测之谓神”，周敦颐《太极图说》更为其注入 “一动一静，互为其根” 的哲学维度。我取 “神火” 意象，实乃融合多重文化血脉：
伏羲氏仰观天象、俯察地法的 “创世火种”——《周易・贲卦》：“观乎天文以察时变”，那团照澈混沌的文明圣火始终在华夏子民血脉中跃动
张载《西铭》“为天地立心” 的生命理想 —— 将 “天工” 与 “人性” 的辩证关系，喻作永不熄灭的纯青炉火
屈原《离骚》“既窈窕以寻壑” 的求索姿态 —— 即使 “路漫漫其修远”，仍要 “指九天以为正” 的不屈魂灵
相较于希腊神话中普罗米修斯盗火的单一神话原型，中文的 “神火” 更多承载着 “天人合一” 的思维印记。这种火的意象：
既是《尚书》“克明峻德” 的修齐治平之道，又如魏源《默觚》所言之 “自反之光，烛照无际”，更暗合禅宗 “一灯能除千年暗” 的顿悟智慧
在翻译过程中，我刻意避免直译 “fated” 的宿命感，转而激活本土典籍中的生命美学：“秉” 字取自《诗经》“执辔如组” 的笃定姿态，“神火” 则令希腊神话的悲剧崇高升华为 “周虽旧邦，其命维新” 的天道信仰 —— 这正是跨语际诗学转化的精髓所在。

尽管可以看出来祂并不了解之前自己的思考过程，但创造的种子已经发芽，祂已能够贯通东西。

总有一天，古往今来所有人类的智慧都会为机器所理解，我们会超越智识的极限，创造出真正的智能。

最后，我想以自己翻译的版本结束这篇文章。

凡人妄图窥探超越其认知之物，实乃愚妄，因此间通往不信与癫狂。
然人者，夙秉神火，注定要超越其身，求索那始终若即若离、难以企及之物。故而当其受挫之时，便会以自身所能理解之事物，去替代那朦胧难明的真理。
若此替代之物，仅能粗略地映照现实本相，纵使已然失真，不也胜过全然无知吗？

匹配的方式有多种，常见的是贪心匹配，效果已经足够好。除此之外还有 SaGe 等算法 ↩
当然现实世界的 Transformer 发展历程不是这样的，直接使用 Embedding 模型可能单纯因为它是已有的成熟技术。但我们的架空世界里还没出现 Embedding 模型。 ↩
虽然不一定是单射，也没有那么严格地保持结构，毕竟我们并不完整地知道词语空间到底长什么样。有人把嵌入定义成高维离散向量映射到低维连续向量，我的意见是 🤷 ↩
Query 和 Key 是同一个子空间，否则若 basis 不同则 Q 和 K 计算的 $QK^T$ 就无意义。 $W_Q$ 和 $W_K$ 是两个不同的，映射到这个空间的线性变换，因此尺寸必然相同。 ↩
假设 $q, k \in \mathbb{R}^{d_k}$ ，它们的元素都是独立同分布的，均值为 0，方差为 1 的随机变量。那么点积 $q \cdot k = \sum_{i=1}^{d_k} q_i k_i$ 的均值仍然是 0，但是其方差会变为 $d_k$ ，因此需要除以 $\sqrt{d_k}$ 来保持方差稳定。 ↩
但 FFN 不只是唯一的记忆了某种知识的构件，自注意力也在一定程度上记忆了关于事物之间关系的知识。 ↩