Here are 10 castles, numbered 1, 2, 3, ... , 10, and worth 1, 2, 3, ... , 10 points respectively. You have 100 soldiers, which you can allocate between the castles however you wish. Your opponent also (independently) does the same. The number of soldiers on each castle is then compared, and for each castle, whoever has the most soldiers on that castle wins its points. Additionally, you lose 0.2 points for each "extra" soldier that you have, in excess of your opponent's army size, at each castle that you win. You still need to deploy all 100 soldiers. In the case of a tie, no one gets points for that castle.
See example below:
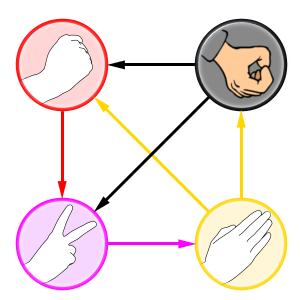
Blotto Example
In this match, Alice wins castles 2, 4, 6, 9 and takes a 6-point penalty, for a total of 15 points, and Carol wins castles 1, 8, 10 and takes a 6-point penalty, for a total of 13 points (no one wins castles 3, 5, 7).
We're going to play a tournament. You get one entry and your final score is the average (mean) of your scores against all the other entries from applicants. An entry should be submitted as a list of 10 non-negative integers, adding up to 100, where the nth element is the number of soldiers being sent to castle n.
What's your entry?
写一个遗传算法在整个行动空间玩大逃杀应该可以得到一个还不错的解.然而在这之外,这个空间上还有没有什么有趣的性质呢?
让我们把问题简化,它本质上是某种剪刀石头布的超级增强版:对于任何一个元素 a a a b b b a < b a < b a < b < < < > > > = = =
那么再向剪刀石头布中加入一个新的元素呢?胜负可能会变成这样:
pierre, papier, ciseaux, puits
尽管每一个元素都会败给另外一个元素,但如果双方随机选择元素,那么有两个元素的胜率是 1 2 \frac{1}{2} 2 1 1 4 \frac{1}{4} 4 1
Remark 1 : 虽然行动空间上可以允许存在 a , b a, b a , b S ( a , b ) = S ( b , a ) S(a, b) = S(b, a) S ( a , b ) = S ( b , a ) 1 , 2 , 3 1, 2, 3 1 , 2 , 3 [ 33 , 33 , 34 ] = [ 40 , 50 , 10 ] [33,33,34] = [40,50,10] [ 33 , 33 , 34 ] = [ 40 , 50 , 10 ] [ 33 , 33 , 34 ] = [ 50 , 40 , 10 ] [33,33,34] = [50,40,10] [ 33 , 33 , 34 ] = [ 50 , 40 , 10 ] [ 40 , 50 , 10 ] ≠ [ 50 , 40 , 10 ] [40,50,10] \neq [50,40,10] [ 40 , 50 , 10 ] = [ 50 , 40 , 10 ]
向问题的行动空间中中加入实数那么多个元素,让可以选择的兵力分布可以是任意的呢?
我们考虑这样一个更一般的情况:两方各拥有 1 1 1 [ 0 , 1 ] [0, 1] [ 0 , 1 ]
假设我方和对方分别从 Δ n \Delta_n Δ n α \alpha α β \beta β S ( α , β ) S(\alpha, \beta) S ( α , β ) R ( α , β ) R(\alpha, \beta) R ( α , β )
S i ( α , β ) = { w i − P ( α i − β i ) α i > β i 0 α i ≤ β i S ( α , β ) = ∑ i = 1 n S i ( α , β ) R i ( α , β ) = S i ( α , β ) − S i ( β , α ) R ( α , β ) = ∑ i = 1 n R i ( α , β ) = S ( α , β ) − S ( β , α ) \begin{aligned} S_i(\alpha, \beta) &= \begin{cases} \begin{aligned} w_i - &P(\alpha_i -\beta_i) &\alpha_i\gt\beta_i\\[4pt] &0 &\alpha_i\leq\beta_i \end{aligned} \end{cases}\\[4pt] S(\alpha, \beta) &= \sum_{i=1}^{n} S_i(\alpha, \beta) \\[16pt] R_i(\alpha, \beta) &= S_i(\alpha, \beta) - S_i(\beta, \alpha) \\[4pt] R(\alpha, \beta) &= \sum_{i=1}^{n} R_i(\alpha, \beta) =S(\alpha, \beta) - S(\beta, \alpha) \end{aligned} S i ( α , β ) S ( α , β ) R i ( α , β ) R ( α , β ) = ⎩ ⎨ ⎧ w i − P ( α i − β i ) 0 α i > β i α i ≤ β i = i = 1 ∑ n S i ( α , β ) = S i ( α , β ) − S i ( β , α ) = i = 1 ∑ n R i ( α , β ) = S ( α , β ) − S ( β , α ) 其中 w i > 0 w_i \gt 0 w i > 0 i i i P P P P ( δ ) = 20 δ P(\delta) = 20\delta P ( δ ) = 20 δ
那么,在对方完全随机选择兵力分布的情况(Δ n \Delta_n Δ n
Theroem 1 Win chance W W W Δ n \Delta_n Δ n n ≥ 1 n \geq 1 n ≥ 1 f ( u ) f(u) f ( u ) Δ n \Delta_n Δ n P ( δ ) P(\delta) P ( δ ) P ( 0 ) = 0 P(0)=0 P ( 0 ) = 0
W : Δ n → [ 0 , 1 ] W ( p ) = ∫ R ( p , u ) > 0 f ( u ) d u \begin{aligned} W:&\text{ }\Delta_n\rightarrow [0,1] \\ W(\mathbf{p}) =& \int_{R(\mathbf{p}, \mathbf{u})>0} f(\mathbf{u})d\mathbf{u} \end{aligned} W : W ( p ) = Δ n → [ 0 , 1 ] ∫ R ( p , u ) > 0 f ( u ) d u Note 1 : 我们略微滥用一下记号,R ( p , u ) > 0 R(\mathbf{p}, \mathbf{u})>0 R ( p , u ) > 0 { u ∣ R ( p , u ) > 0 , u ∈ Δ n } \{\mathbf{u} \mid R(\mathbf{p}, \mathbf{u})>0, \mathbf{u} \in \Delta_n\} { u ∣ R ( p , u ) > 0 , u ∈ Δ n } p \mathbf{p} p u \mathbf{u} u 0 0 0 d u = d u 1 d u 2 . . . d u n d\mathbf{u}=du_1du_2...du_n d u = d u 1 d u 2 ... d u n
Note 2 : 并且「连续」还不能保证 w i − P ( ϵ i ) w_i - P(\epsilon_i) w i − P ( ϵ i ) ϵ \boldsymbol{\epsilon} ϵ P ( ϵ i ) < w i P(\epsilon_i)<w_i P ( ϵ i ) < w i S i S_i S i P P P
任取一点 p ∈ Δ n \mathbf{p} \in \Delta_n p ∈ Δ n ∀ δ > 0 , ∃ ϵ , ∣ W ( p + ϵ ) − W ( p ) ∣ < δ \forall \delta > 0\text{, }\exists\boldsymbol{\epsilon}\text{, }|W(\mathbf{p}+\boldsymbol{\epsilon}) - W(\mathbf{p})| < \delta ∀ δ > 0 , ∃ ϵ , ∣ W ( p + ϵ ) − W ( p ) ∣ < δ
这实际上有些困难,对于每一点 p \mathbf{p} p p \mathbf{p} p Δ n \Delta_n Δ n ϵ \boldsymbol{\epsilon} ϵ
∑ i = 1 n ϵ i = 0 \sum_{i=1}^n \epsilon_i = 0 i = 1 ∑ n ϵ i = 0 p + ϵ ∈ Δ n \mathbf{p}+\boldsymbol{\epsilon} \in \Delta_n p + ϵ ∈ Δ n 并且相对得分 R ( p + ϵ , p ) R(\mathbf{p}+\boldsymbol{\epsilon}, \mathbf{p}) R ( p + ϵ , p ) p \mathbf{p} p
R ( p + ϵ , p ) = ∑ i = 1 n w i ⋅ s g n ( ϵ i ) − P ( ϵ i ) R(\mathbf{p}+\boldsymbol{\epsilon}, \mathbf{p}) = \sum_{i=1}^n w_i \cdot \mathrm{sgn}(\epsilon_i)-P(\epsilon_i) R ( p + ϵ , p ) = i = 1 ∑ n w i ⋅ sgn ( ϵ i ) − P ( ϵ i ) 即使我们有假设 P ( ϵ ) P(\boldsymbol{\epsilon}) P ( ϵ ) ϵ → 0 \boldsymbol{\epsilon} \rightarrow 0 ϵ → 0 P ( ϵ ) → 0 P(\boldsymbol{\epsilon}) \rightarrow 0 P ( ϵ ) → 0 R R R p \mathbf{p} p ϵ i \epsilon_i ϵ i
我画了一个 Δ 3 \Delta_3 Δ 3 R ( p + ϵ , p ) R(\mathbf{p}+\boldsymbol\epsilon, \mathbf{p}) R ( p + ϵ , p )
Relative score on Δ₃
一开始我也认为为胜率或许并不连续,不过一天多之后我找到了证明思路.要证明胜率变化的连续性,其实我们只需要关注获胜区域的变化,也就是与 p \mathbf{p} p p + ϵ \mathbf{p}+\boldsymbol{\epsilon} p + ϵ
接下来我要宣称,从 p \mathbf{p} p p + ϵ \mathbf{p}+\boldsymbol{\epsilon} p + ϵ 全部 落在某个特定区域内.
让我们固定其他分量,只看某一个维度的变化.我们将 p \mathbf{p} p i i i
Projection
对于 inf α i > max ( p i , p i + ϵ i ) \inf \alpha_i \gt \max(p_i, p_i+\epsilon_i) inf α i > max ( p i , p i + ϵ i ) i i i p \mathbf{p} p w i w_i w i 对于 sup β i < min ( p i , p i + ϵ i ) \sup \beta_i \lt \min(p_i, p_i+\epsilon_i) sup β i < min ( p i , p i + ϵ i ) i i i w i w_i w i 实际上如果 ϵ i > 0 \epsilon_i>0 ϵ i > 0 p \mathbf{p} p p i p_i p i p i + ϵ i p_i + \epsilon_i p i + ϵ i [ p i , p i + ϵ i ] [p_i, p_i + \epsilon_i] [ p i , p i + ϵ i ] ϵ i < 0 \epsilon_i<0 ϵ i < 0 [ p i − ϵ i , p i ] [p_i - \epsilon_i, p_i] [ p i − ϵ i , p i ]
Proposition 1 If R ( p , u ) ≠ R ( p + ϵ , u ) R(\mathbf{p}, \mathbf{u}) \neq R(\mathbf{p}+\boldsymbol{\epsilon}, \mathbf{u}) R ( p , u ) = R ( p + ϵ , u ) p \mathbf{p} p P ( ϵ i ) < w i P(\epsilon_i)<w_i P ( ϵ i ) < w i u ∈ ∏ i = 1 n [ p i , p i + ϵ i ) \mathbf{u} \in \prod_{i=1}^n [p_i, p_i+\epsilon_i) u ∈ ∏ i = 1 n [ p i , p i + ϵ i )
我们记
I + = { i ∣ ϵ i > 0 } I^+ = \{i \mid \epsilon_i > 0\} I + = { i ∣ ϵ i > 0 } ϵ i \epsilon_i ϵ i i i i I − = { i ∣ ϵ i < 0 } I^- = \{i \mid \epsilon_i < 0\} I − = { i ∣ ϵ i < 0 } ϵ i \epsilon_i ϵ i i i i V p = { u ∣ R ( p , u ) > 0 } \mathcal{V}_p = \{\mathbf{u} \mid R(\mathbf{p}, \mathbf{u})>0\} V p = { u ∣ R ( p , u ) > 0 } p \mathbf{p} p V p + ϵ = { u ∣ R ( p + ϵ , u ) > 0 } \mathcal{V}_{p+\epsilon} = \{\mathbf{u} \mid R(\mathbf{p+\boldsymbol\epsilon}, \mathbf{u})>0\} V p + ϵ = { u ∣ R ( p + ϵ , u ) > 0 } p + ϵ \mathbf{p}+\boldsymbol{\epsilon} p + ϵ V i + = Δ n ∩ ( R i − 1 × [ p i , p i + ϵ i ) × R n − i − 1 ) , i ∈ I + \mathcal{V}_i^+ = \Delta_n \cap (\mathbb{R}^{i-1} \times [p_i, p_i + \epsilon_i) \times \mathbb{R}^{n-i-1}), i \in I^+ V i + = Δ n ∩ ( R i − 1 × [ p i , p i + ϵ i ) × R n − i − 1 ) , i ∈ I + V i − = Δ n ∩ ( R i − 1 × ( p i + ϵ i , p i ] × R n − i − 1 ) , i ∈ I − \mathcal{V}_i^- = \Delta_n \cap (\mathbb{R}^{i-1} \times (p_i + \epsilon_i, p_i] \times \mathbb{R}^{n-i-1}), i \in I^- V i − = Δ n ∩ ( R i − 1 × ( p i + ϵ i , p i ] × R n − i − 1 ) , i ∈ I − 那么获胜概率的变化为:
W ( p + ϵ ) − W ( p ) = ∫ V p + ϵ f ( u ) d u − ∫ V p f ( u ) d u = ∫ V p + ϵ ∖ V p f ( u ) d u + ∫ V p + ϵ ∩ V p f ( u ) d u − ∫ V p ∖ V p + ϵ f ( u ) d u − ∫ V p + ϵ ∩ V p f ( u ) d u = ∫ V p + ϵ ∖ V p f ( u ) d u − ∫ V p ∖ V p + ϵ f ( u ) d u = ∫ ⋃ i ∈ I + ( V p + ϵ ∩ V i + ) f ( u ) d u − ∫ ⋃ i ∈ I − ( V p + ϵ ∩ V i − ) f ( u ) d u \begin{align} W(\mathbf{p}+\boldsymbol\epsilon) - W(\mathbf{p})=& \int_{\mathcal{V}_{p+\epsilon}} f(\mathbf{u})d\mathbf{u} - \int_{\mathcal{V}_{p}} f(\mathbf{u})d\mathbf{u}\\ =& \int_{\mathcal{V}_{p+\epsilon}\setminus \mathcal{V}_{p}} f(\mathbf{u})d\mathbf{u} + \int_{\mathcal{V}_{p+\epsilon} \cap \mathcal{V}_{p}} f(\mathbf{u})d\mathbf{u}\\ &- \int_{\mathcal{V}_{p}\setminus \mathcal{V}_{p+\epsilon}} f(\mathbf{u})d\mathbf{u} - \int_{\mathcal{V}_{p+\epsilon} \cap \mathcal{V}_{p}} f(\mathbf{u})d\mathbf{u}\notag\\ =& \int_{\mathcal{V}_{p+\epsilon}\setminus \mathcal{V}_{p}} f(\mathbf{u})d\mathbf{u} - \int_{\mathcal{V}_{p}\setminus \mathcal{V}_{p+\epsilon}} f(\mathbf{u})d\mathbf{u}\\ =&\int_{\bigcup_{i \in I^+}(\mathcal{V}_{p+\epsilon}\cap\mathcal{V}_i^+)} f(\mathbf{u})d\mathbf{u} - \int_{\bigcup_{i \in I^-}(\mathcal{V}_{p+\epsilon}\cap\mathcal{V}_i^-)} f(\mathbf{u})d\mathbf{u}\\ \end{align} W ( p + ϵ ) − W ( p ) = = = = ∫ V p + ϵ f ( u ) d u − ∫ V p f ( u ) d u ∫ V p + ϵ ∖ V p f ( u ) d u + ∫ V p + ϵ ∩ V p f ( u ) d u − ∫ V p ∖ V p + ϵ f ( u ) d u − ∫ V p + ϵ ∩ V p f ( u ) d u ∫ V p + ϵ ∖ V p f ( u ) d u − ∫ V p ∖ V p + ϵ f ( u ) d u ∫ ⋃ i ∈ I + ( V p + ϵ ∩ V i + ) f ( u ) d u − ∫ ⋃ i ∈ I − ( V p + ϵ ∩ V i − ) f ( u ) d u ( 2 ) (2) ( 2 ) S i S_i S i ∫ ⋃ S i f d μ = ∑ ∫ S i f d μ \int_{\bigcup S_i} f d\mu = \sum \int_{S_i} f d\mu ∫ ⋃ S i fd μ = ∑ ∫ S i fd μ X = ( X ∖ Y ) ∪ ( X ∩ Y ) X = (X \setminus Y) \cup (X \cap Y) X = ( X ∖ Y ) ∪ ( X ∩ Y )
( 3 ) (3) ( 3 ) ( 2 ) (2) ( 2 ) V p \mathcal{V}_p V p V p + ϵ \mathcal{V}_{p+\epsilon} V p + ϵ
( 4 ) (4) ( 4 ) Proposition 1 ,胜负会变化的点一定落在这些区域内.并且我们已知,这两个区域不相交.
我们来单独看其中一部分:
∫ ⋃ i ∈ I + ( V p + ϵ ∩ V i + ) f ( u ) d u = ∑ i ∈ I + ∫ V p + ϵ ∩ V i + f ( u ) d u ≤ ∑ i ∈ I + ∫ V i + f ( u ) d u = ∑ i ∈ I + ∫ V i + d u V o l ( Δ n ) = ∑ i ∈ I + V o l ( V i + ) V o l ( Δ n ) = 1 V o l ( Δ n ) ∑ i ∈ I + ∫ p i p i + ϵ i ( 1 − p ) n − 1 ⋅ V o l ( Δ n − 1 ) d p = V o l ( Δ n − 1 ) V o l ( Δ n ) ∑ i ∈ I + ∫ p i p i + ϵ i ( 1 − p ) n − 1 d p = V o l ( Δ n − 1 ) V o l ( Δ n ) ∑ i ∈ I + ( − ( 1 − p ) n n ) ∣ p i p i + ϵ i \begin{align} \int_{\bigcup_{i \in I^+}(\mathcal{V}_{p+\epsilon}\cap\mathcal{V}_i^+)} f(\mathbf{u})d\mathbf{u} =& \sum_{i \in I^+} \int_{\mathcal{V}_{p+\epsilon}\cap\mathcal{V}_i^+} f(\mathbf{u})d\mathbf{u}\\ \leq& \sum_{i \in I^+} \int_{\mathcal{V}_i^+} f(\mathbf{u})d\mathbf{u}\\ =& \sum_{i \in I^+} \int_{\mathcal{V}_i^+} \frac{d\mathbf{u}}{\mathrm{Vol}(\Delta_n)} \\ =& \sum_{i \in I^+} \frac{\mathrm{Vol}(\mathcal{V}_i^+)}{\mathrm{Vol}(\Delta_n)} \\ =& \frac{1}{\mathrm{Vol}(\Delta_n)} \sum_{i \in I^+} \int_{p_i}^{p_i+\epsilon_i} (1-p)^{n-1} \cdot \mathrm{Vol}(\Delta_{n-1})dp \\ =& \frac{\mathrm{Vol}(\Delta_{n-1})}{\mathrm{Vol}(\Delta_n)} \sum_{i \in I^+} \int_{p_i}^{p_i+\epsilon_i} (1-p)^{n-1} dp\\ =& \frac{\mathrm{Vol}(\Delta_{n-1})}{\mathrm{Vol}(\Delta_n)} \sum_{i \in I^+} \left(-\frac{(1-p)^{n}}{n}\right) \bigg\vert_{p_i}^{p_i+\epsilon_i} \end{align} ∫ ⋃ i ∈ I + ( V p + ϵ ∩ V i + ) f ( u ) d u = ≤ = = = = = i ∈ I + ∑ ∫ V p + ϵ ∩ V i + f ( u ) d u i ∈ I + ∑ ∫ V i + f ( u ) d u i ∈ I + ∑ ∫ V i + Vol ( Δ n ) d u i ∈ I + ∑ Vol ( Δ n ) Vol ( V i + ) Vol ( Δ n ) 1 i ∈ I + ∑ ∫ p i p i + ϵ i ( 1 − p ) n − 1 ⋅ Vol ( Δ n − 1 ) d p Vol ( Δ n ) Vol ( Δ n − 1 ) i ∈ I + ∑ ∫ p i p i + ϵ i ( 1 − p ) n − 1 d p Vol ( Δ n ) Vol ( Δ n − 1 ) i ∈ I + ∑ ( − n ( 1 − p ) n ) p i p i + ϵ i ( 5 ) (5) ( 5 )
( 6 ) (6) ( 6 ) f ( u ) ≥ 0 f(\mathbf{u}) \geq 0 f ( u ) ≥ 0
( 7 ) (7) ( 7 ) f ( u ) = 1 / V o l ( Δ n ) f(\mathbf{u}) = {1}/{\mathrm{Vol}(\Delta_n)} f ( u ) = 1 / Vol ( Δ n ) Δ n \Delta_n Δ n V o l ( Δ n ) \mathrm{Vol}(\Delta_n) Vol ( Δ n ) Δ n \Delta_n Δ n
( 8 ) (8) ( 8 ) V i + = Δ n ∩ ( R i − 1 × [ p i , p i + ϵ i ) × R n − i ) \mathcal{V}_i^+ = \Delta_n \cap (\mathbb{R}^{i-1} \times [p_i, p_i + \epsilon_i) \times \mathbb{R}^{n-i}) V i + = Δ n ∩ ( R i − 1 × [ p i , p i + ϵ i ) × R n − i ) n n n p i p_i p i p i + ϵ i p_i+\epsilon_i p i + ϵ i n − 1 n-1 n − 1
( 9 ) (9) ( 9 ) V o l ( Δ n − 1 ) \mathrm{Vol}(\Delta_{n-1}) Vol ( Δ n − 1 ) ( 10 ) (10) ( 10 )
同理我们有
∫ ⋃ i ∈ I ( V p + ϵ ∩ V i − ) f ( u ) d u ≤ V o l ( Δ n − 1 ) V o l ( Δ n ) ∑ i ∈ I − ( − ( 1 − p ) n n ) ∣ p i + ϵ i p i \int_{\bigcup_{i \in I}(\mathcal{V}_{p+\epsilon}\cap\mathcal{V}_i^-)} f(\mathbf{u})d\mathbf{u} \leq \frac{\mathrm{Vol}(\Delta_{n-1})}{\mathrm{Vol}(\Delta_n)} \sum_{i \in I^-} \left(-\frac{(1-p)^{n}}{n}\right) \bigg\vert_{p_i+\epsilon_i}^{p_i} ∫ ⋃ i ∈ I ( V p + ϵ ∩ V i − ) f ( u ) d u ≤ Vol ( Δ n ) Vol ( Δ n − 1 ) i ∈ I − ∑ ( − n ( 1 − p ) n ) p i + ϵ i p i 并且由于 ∣ a − b ∣ ≤ ∣ a ∣ + ∣ b ∣ |a-b| \leq |a|+|b| ∣ a − b ∣ ≤ ∣ a ∣ + ∣ b ∣
∣ W ( p + ϵ ) − W ( p ) ∣ ≤ V o l ( Δ n − 1 ) V o l ( Δ n ) ( ∣ ∑ i ∈ I + ( − ( 1 − p ) n n ) ∣ p i p i + ϵ i ∣ + ∣ ∑ i ∈ I − ( − ( 1 − p ) n n ) ∣ p i + ϵ i p i ∣ ) = n + 1 n ( ∣ ∑ i ∈ I + ( 1 − p ) n ∣ p i p i + ϵ i ∣ + ∣ ∑ i ∈ I − ( 1 − p ) n ∣ p i + ϵ i p i ∣ ) \begin{align} |W(\mathbf{p}+\boldsymbol\epsilon) - W(\mathbf{p})| \leq& \frac{\mathrm{Vol}(\Delta_{n-1})}{\mathrm{Vol}(\Delta_n)} \left(\left|\sum_{i \in I^+} \left(-\frac{(1-p)^{n}}{n}\right) \bigg\vert_{p_i}^{p_i+\epsilon_i}\right| + \left|\sum_{i \in I^-} \left(-\frac{(1-p)^{n}}{n}\right) \bigg\vert_{p_i+\epsilon_i}^{p_i}\right|\right) \\ =& \frac{n+1}{n} \left(\left|\sum_{i \in I^+} {(1-p)^{n}} \big\vert_{p_i}^{p_i+\epsilon_i}\right| + \left|\sum_{i \in I^-} {(1-p)^{n}} \big\vert_{p_i+\epsilon_i}^{p_i}\right|\right)\\ \end{align} ∣ W ( p + ϵ ) − W ( p ) ∣ ≤ = Vol ( Δ n ) Vol ( Δ n − 1 ) ( i ∈ I + ∑ ( − n ( 1 − p ) n ) p i p i + ϵ i + i ∈ I − ∑ ( − n ( 1 − p ) n ) p i + ϵ i p i ) n n + 1 ( i ∈ I + ∑ ( 1 − p ) n p i p i + ϵ i + i ∈ I − ∑ ( 1 − p ) n p i + ϵ i p i ) 右侧是一个关于 p i p_i p i ϵ i \epsilon_i ϵ i ϵ → 0 \boldsymbol\epsilon \rightarrow 0 ϵ → 0 0 0 0
∀ δ > 0 , ∃ ϵ , s.t. ∣ W ( p + ϵ ) − W ( p ) ∣ < δ . \forall \delta > 0, \exists \, \boldsymbol{\epsilon}, \text{ s.t. } |W(\mathbf{p} + \boldsymbol{\epsilon}) - W(\mathbf{p})| < \delta. ∀ δ > 0 , ∃ ϵ , s.t. ∣ W ( p + ϵ ) − W ( p ) ∣ < δ . 由于 p \mathbf{p} p Δ n \Delta_n Δ n W W W Δ n \Delta_n Δ n
至此我们已经证明了对任意有限 n n n n = ∞ n = \infty n = ∞
当然这个结论对任意可以对有界 PDF 有效,只需要在证明过程保留 f ( u ) f(\mathbf{u}) f ( u ) f ( u ) = 0 when u ∉ d o m f f(\mathbf{u}) = 0 \text{ when } \mathbf{u} \notin \mathrm{dom}f f ( u ) = 0 when u ∈ / dom f
那么原本的题目 (离散 Blotto Game) 呢?直觉上来说我们只需要将总兵力作为单位 1 1 1 ϵ i ≤ 0.005 \epsilon_i \leq 0.005 ϵ i ≤ 0.005
∣ W ( p + ϵ ) − W ( p ) ∣ ≤ 11 10 ∑ i = 1 10 ∣ ( 1 − p ) 10 ∣ p i p i + ϵ i ∣ ≤ 11 10 ∑ i = 1 10 ∣ ( 0.995 − p i ) 10 − ( 1 − p i ) 10 ∣ ≈ 11 10 ∑ i = 1 10 ∣ − 0.0489 + 0.441 p i − 1.769 p i 2 + 4.138 p i 3 + O ( p i 4 ) ∣ ⪅ 53.78 % \begin{align*} |W(\mathbf{p}+\boldsymbol\epsilon) - W(\mathbf{p})| \leq& \frac{11}{10} \sum_{i=1}^{10} \left|{(1-p)^{10}} \big\vert_{p_i}^{p_i+\epsilon_i}\right| \\ \leq& \frac{11}{10} \sum_{i=1}^{10} \left|{(0.995-p_i)^{10}} - (1-p_i)^{10}\right| \\ \approx& \frac{11}{10} \sum_{i=1}^{10} |-0.0489+0.441p_i-1.769p_i^2+4.138p_i^3+\mathcal{O}(p_i^4)| \\[8pt] \lessapprox&\text{ }53.78\% \end{align*} ∣ W ( p + ϵ ) − W ( p ) ∣ ≤ ≤ ≈ ⪅ 10 11 i = 1 ∑ 10 ( 1 − p ) 10 p i p i + ϵ i 10 11 i = 1 ∑ 10 ( 0.995 − p i ) 10 − ( 1 − p i ) 10 10 11 i = 1 ∑ 10 ∣ − 0.0489 + 0.441 p i − 1.769 p i 2 + 4.138 p i 3 + O ( p i 4 ) ∣ 53.78% 你的不等式十分紧致,但是又相当松弛.
私密马赛,我们还得找到一个更精细的上界.问题出在 ∣ a − b ∣ ≤ ∣ a ∣ + ∣ b ∣ |a-b| \leq |a|+|b| ∣ a − b ∣ ≤ ∣ a ∣ + ∣ b ∣
∣ W ( p + ϵ ) − W ( p ) ∣ ≤ 11 10 ∣ ∑ i = 1 10 − ( 1 − p ) 10 ∣ p i p i + ϵ i ∣ \begin{align*} |W(\mathbf{p}+\boldsymbol\epsilon) - W(\mathbf{p})| \leq& \frac{11}{10} \left|\sum_{i=1}^{10} -{(1-p)^{10}} \big\vert_{p_i}^{p_i+\epsilon_i}\right| \\ \end{align*} ∣ W ( p + ϵ ) − W ( p ) ∣ ≤ 10 11 i = 1 ∑ 10 − ( 1 − p ) 10 p i p i + ϵ i 这里有一个直观的意义:− ( 1 − p ) 10 ∣ p i p i + ϵ i -{(1-p)^{10}} \big\vert_{p_i}^{p_i+\epsilon_i} − ( 1 − p ) 10 p i p i + ϵ i f ( x ) = ( 1 − x ) 11 11 f(x)=\frac{(1-x)^{11}}{11} f ( x ) = 11 ( 1 − x ) 11 x = p i x=p_i x = p i x = p i + ϵ i x=p_i+\epsilon_i x = p i + ϵ i 0 0 0 ∑ i = 1 10 ϵ i = 0 \sum_{i=1}^{10} \epsilon_i = 0 ∑ i = 1 10 ϵ i = 0 0 0 0
计算一下每一项对 p i p_i p i
∂ ( ( 1 − p i ) 10 − ( 1 − p i − ϵ i ) 10 ) ∂ p i = 10 ( 1 − p i − ϵ i ) 9 − 10 ( 1 − p i ) 9 \frac{\partial \left( (1-p_i)^{10}-(1-p_i-\epsilon_i)^{10} \right)}{\partial p_i} = 10(1-p_i-\epsilon_i)^9-10(1-p_i)^9 ∂ p i ∂ ( ( 1 − p i ) 10 − ( 1 − p i − ϵ i ) 10 ) = 10 ( 1 − p i − ϵ i ) 9 − 10 ( 1 − p i ) 9 符号与 ϵ i \epsilon_i ϵ i i ∈ I + i \in I^+ i ∈ I + p i p_i p i i ∈ I − i \in I^- i ∈ I − p i p_i p i p i = 0 , i ∈ I + p_i = 0, i \in I^+ p i = 0 , i ∈ I + ∑ i ∈ I − p i = 1 \sum_{i \in I^-} p_i = 1 ∑ i ∈ I − p i = 1
而 ϵ i \epsilon_i ϵ i p i + ϵ i p_i + \epsilon_i p i + ϵ i p i p_i p i ∑ i = 1 10 ϵ i = 0 \sum_{i=1}^{10} \epsilon_i = 0 ∑ i = 1 10 ϵ i = 0 5 5 5 0.005 0.005 0.005 5 5 5 − 0.005 -0.005 − 0.005 ≈ 20.75 % \approx 20.75\% ≈ 20.75% p = [ 0 , 0 , 0 , 0 , 0 , 0.2 , 0.2 , 0.2 , 0.2 , 0.2 ] \mathbf{p} = [0,0,0,0,0,0.2,0.2,0.2,0.2,0.2] p = [ 0 , 0 , 0 , 0 , 0 , 0.2 , 0.2 , 0.2 , 0.2 , 0.2 ] ϵ = [ 0.05 , 0.05 , 0.05 , 0.05 , 0.05 , − 0.05 , − 0.05 , − 0.05 , − 0.05 , − 0.05 ] \boldsymbol{\epsilon} = [0.05,0.05,0.05,0.05,0.05,-0.05,-0.05,-0.05,-0.05,-0.05] ϵ = [ 0.05 , 0.05 , 0.05 , 0.05 , 0.05 , − 0.05 , − 0.05 , − 0.05 , − 0.05 , − 0.05 ]
不过「胜率最高点」附近的胜率变化可能不会如此陡峭,在 p = [ 0.1 , 0.1 , 0.1 , 0.1 , 0.1 , 0.1 , 0.1 , 0.1 , 0.1 , 0.1 ] \mathbf{p} = [0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1] p = [ 0.1 , 0.1 , 0.1 , 0.1 , 0.1 , 0.1 , 0.1 , 0.1 , 0.1 , 0.1 ] ≈ 1.04 % \approx 1.04\% ≈ 1.04% n n n
不过这是一个博弈,我们还需要估计对手类型的分布.我们可以很容易得到胜率的链式法则:
Theorem 2 For a two-player continuous blotto game with bounded probability density function f f f W f W_f W f f f f W p ∘ ( f 1 , . . . f n ) ( u ) = ∑ i = 1 n p i W f i ( u ) W_{\mathbf{p}\circ(f_1,...f_n)}(\mathbf{u}) = \sum_{i=1}^{n} p_i W_{f_i}(\mathbf{u}) W p ∘ ( f 1 , ... f n ) ( u ) = ∑ i = 1 n p i W f i ( u ) for all p ∈ Δ n \mathbf{p} \in \Delta_n p ∈ Δ n
Proof :
W p ∘ ( f 1 , . . . f n ) ( u ) = ∫ R ( u , v ) > 0 ( p ∘ ( f 1 , . . . f n ) ) ( v ) d v = ∫ R ( u , v ) > 0 ∑ i = 1 n p i f i ( v ) d v = ∑ i = 1 n ∫ R ( u , v ) > 0 p i f i ( v ) d v = ∑ i = 1 n p i W f i ( u ) \begin{align} W_{\mathbf{p}\circ(f_1,...f_n)}(\mathbf{u}) =& \int_{R(\mathbf{u}, \mathbf{v})>0} (\mathbf{p}\circ(f_1,...f_n))(\mathbf{v})d\mathbf{v} \\ =& \int_{R(\mathbf{u}, \mathbf{v})>0} \sum_{i=1}^{n} p_i f_i(\mathbf{v})d\mathbf{v} \\ =& \sum_{i=1}^{n} \int_{R(\mathbf{u}, \mathbf{v})>0} p_i f_i(\mathbf{v}) d\mathbf{v} \\ =& \sum_{i=1}^{n} p_i W_{f_i}(\mathbf{u}) \end{align} W p ∘ ( f 1 , ... f n ) ( u ) = = = = ∫ R ( u , v ) > 0 ( p ∘ ( f 1 , ... f n )) ( v ) d v ∫ R ( u , v ) > 0 i = 1 ∑ n p i f i ( v ) d v i = 1 ∑ n ∫ R ( u , v ) > 0 p i f i ( v ) d v i = 1 ∑ n p i W f i ( u ) ( 16 ) (16) ( 16 )
Remark 2 : It applies to discrete and mixed distributions as we change the integral to sum.
比如我们可以假设有 50% 的人会靠直觉在每个城堡都布置一点兵力,兵力分布与城堡分数正相关;30% 的人会考虑到第一层,利用某种算法得到胜率的一些极值点附近的区域;15% 的人会考虑到有聪明的对手和不太聪明的对手;还有 5% 的人会或许会出奇招梭哈赌一把.最终面对所有对手的胜率会是单独面对各类对手的胜率的简单线性组合.
那么期望得分呢?
E [ S ( p ) ] = ∫ Δ n S ( p , u ) f ( u ) d u \mathbb{E}[S(\mathbf{p})] = \int_{\Delta_n} S(\mathbf{p}, \mathbf{u})f(\mathbf{u})d\mathbf{u} E [ S ( p )] = ∫ Δ n S ( p , u ) f ( u ) d u 我们有 ∀ w i > 0 , ∃ ϵ , P ( ϵ i ) < w i \forall w_i > 0\text{, }\exists\boldsymbol{\epsilon}\text{, } P(\epsilon_i) < w_i ∀ w i > 0 , ∃ ϵ , P ( ϵ i ) < w i
E [ S ( p + ϵ ) ] − E [ S ( p ) ] = ∫ Δ n S ( p + ϵ , u ) f ( u ) d u − ∫ Δ n S ( p , u ) f ( u ) d u = ∫ Δ n ( S ( p + ϵ , u ) − S ( p , u ) ) f ( u ) d u = ∫ ∏ i = 1 n [ p i , p i + ϵ i ) ( S ( p + ϵ , u ) − S ( p , u ) ) f ( u ) d u + ∫ Δ n ∖ ( ∏ i = 1 n [ p i , p i + ϵ i ) ) ( S ( p + ϵ , u ) − S ( p , u ) ) f ( u ) d u ≤ ∫ ∏ i = 1 n [ p i , p i + ϵ i ) max S f ( u ) d u \begin{align} \mathbb{E}[S(\mathbf{p}+\boldsymbol\epsilon)] - \mathbb{E}[S(\mathbf{p})] =& \int_{\Delta_n} S(\mathbf{p}+\boldsymbol\epsilon, \mathbf{u})f(\mathbf{u})d\mathbf{u} -\int_{\Delta_n} S(\mathbf{p}, \mathbf{u})f(\mathbf{u})d\mathbf{u} \\ =& \int_{\Delta_n} (S(\mathbf{p}+\boldsymbol\epsilon, \mathbf{u})-S(\mathbf{p}, \mathbf{u})) f(\mathbf{u})d\mathbf{u} \\ =& \int_{\prod_{i=1}^n [p_i, p_i+\epsilon_i)} (S(\mathbf{p}+\boldsymbol\epsilon, \mathbf{u})-S(\mathbf{p}, \mathbf{u}))f(\mathbf{u})d\mathbf{u} \\ &+ \int_{\Delta_n\setminus(\prod_{i=1}^n [p_i, p_i+\epsilon_i))} (S(\mathbf{p}+\boldsymbol\epsilon, \mathbf{u})-S(\mathbf{p}, \mathbf{u}))f(\mathbf{u})d\mathbf{u} \\ \leq& \int_{\prod_{i=1}^n [p_i, p_i+\epsilon_i)} \max{S}f(\mathbf{u})d\mathbf{u} \\ \end{align} E [ S ( p + ϵ )] − E [ S ( p )] = = = ≤ ∫ Δ n S ( p + ϵ , u ) f ( u ) d u − ∫ Δ n S ( p , u ) f ( u ) d u ∫ Δ n ( S ( p + ϵ , u ) − S ( p , u )) f ( u ) d u ∫ ∏ i = 1 n [ p i , p i + ϵ i ) ( S ( p + ϵ , u ) − S ( p , u )) f ( u ) d u + ∫ Δ n ∖ ( ∏ i = 1 n [ p i , p i + ϵ i )) ( S ( p + ϵ , u ) − S ( p , u )) f ( u ) d u ∫ ∏ i = 1 n [ p i , p i + ϵ i ) max S f ( u ) d u ( 22 ) (22) ( 22 ) Proposition 1 Δ n ∖ ( ∏ i = 1 n [ p i , p i + ϵ i ) ) \Delta_n\setminus\big(\prod_{i=1}^n [p_i, p_i+\epsilon_i)\big) Δ n ∖ ( ∏ i = 1 n [ p i , p i + ϵ i ) ) S ( p + ϵ , u ) − S ( p , u ) = 0 S(\mathbf{p}+\boldsymbol\epsilon, \mathbf{u})-S(\mathbf{p}, \mathbf{u}) = 0 S ( p + ϵ , u ) − S ( p , u ) = 0 m a x S \mathrm{max}S max S S i S_i S i
当然也是连续的.美丽!
“色魔啊色魔,你又作伪证了! ”色魔刚把文章发出来,所有喝酒的人便都看著他笑. 色魔瞪大眼睛:“你怎么这样凭空污人清白!”“什么清白?我亲眼见你在 R n \mathbb{R}^n R n
Indeed,我们需要证明,对任意 p ∈ Δ n \mathbf{p} \in \Delta_n p ∈ Δ n V + = { u ∣ R ( p , u ) > 0 , u ∈ Δ n } \mathcal{V}^+=\{\mathbf{u} \mid R(\mathbf{p}, \mathbf{u})>0, \mathbf{u} \in \Delta_n\} V + = { u ∣ R ( p , u ) > 0 , u ∈ Δ n }
我们还是把 V + \mathcal{V}^+ V + P ( δ ) = 0 P(\delta) = 0 P ( δ ) = 0 i i i
p i > u i , R i > 0 p_i>u_i, R_i>0 p i > u i , R i > 0 p i ≤ u i , R i = 0 p_i \leq u_i, R_i=0 p i ≤ u i , R i = 0 对每个分量 i i i Δ n \Delta_n Δ n p i > u i p_i>u_i p i > u i p i ≤ u i p_i \leq u_i p i ≤ u i 2 n 2^n 2 n
在有惩罚函数的情况下,情况似乎会复杂一些.即使 p i > u i p_i>u_i p i > u i R i = S i ( p , u ) − S i ( u , p ) R_i = S_i(\mathbf{p}, \mathbf{u}) - S_i(\mathbf{u}, \mathbf{p}) R i = S i ( p , u ) − S i ( u , p ) = s g n ( p i − u i ) ( w i − P ( p i − u i ) ) =sgn(p_i-u_i)\left(w_i - P(p_i-u_i)\right) = s g n ( p i − u i ) ( w i − P ( p i − u i ) ) ≤ 0 \leq0 ≤ 0
但我们有假设 P ( δ ) P(\delta) P ( δ ) R i R_i R i ( 0 , ∞ ) (0,\infty) ( 0 , ∞ ) R i − 1 ( p , u ) R_i^{-1}(\mathbf{p}, \mathbf{u}) R i − 1 ( p , u ) 1
A set E ⊆ R n E \subseteq \mathbb{R}^n E ⊆ R n ϵ > 0 \epsilon > 0 ϵ > 0 O O O
E ⊆ O and m ∗ ( O ∖ E ) < ϵ E \subseteq O \quad \text{and} \quad m^*(O \setminus E) < \epsilon E ⊆ O and m ∗ ( O ∖ E ) < ϵ where m ∗ m^* m ∗
因为,平凡地,R n \mathbb{R}^n R n O = E O=E O = E m ∗ ( O ∖ E ) = m ∗ ( ∅ ) = 0 < ϵ m^*(O \setminus E) = m^*(\emptyset) = 0 < \epsilon m ∗ ( O ∖ E ) = m ∗ ( ∅ ) = 0 < ϵ 2
接下来同样的,可数个可测集的笛卡尔积 ∏ i = 1 n R i − 1 ( p , u ) \prod_{i=1}^n R_i^{-1}(\mathbf{p}, \mathbf{u}) ∏ i = 1 n R i − 1 ( p , u ) V + \mathcal{V}^+ V +

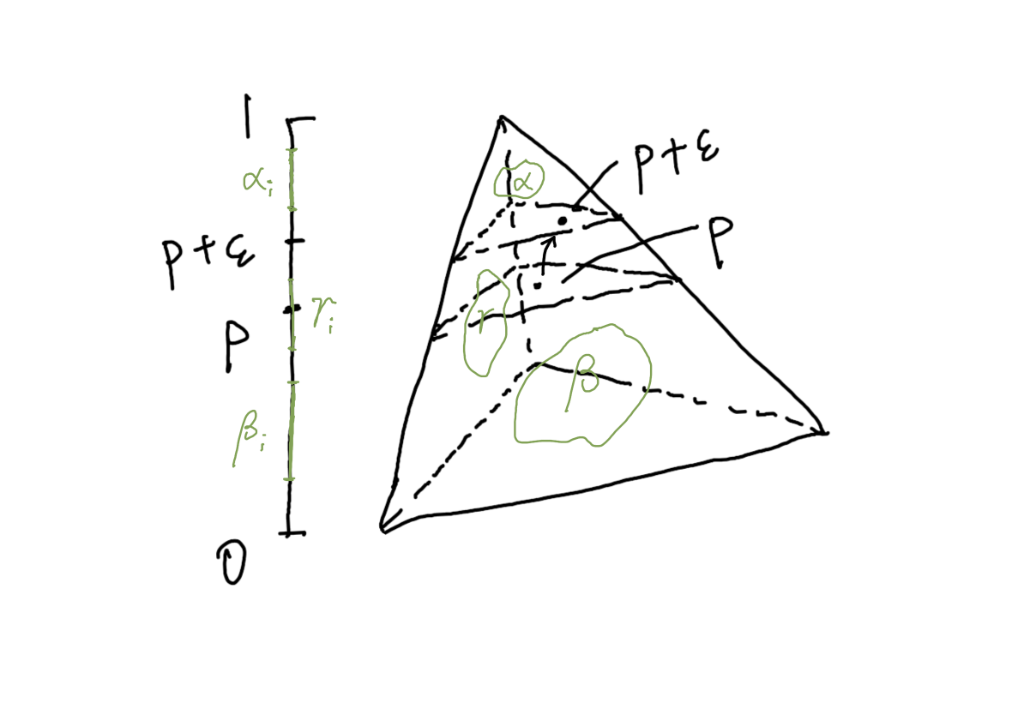

博主,建議檢查一下博客,當前博文從中間劃分,右邊全為空白。其他博文沒有關係。